Und bedenken Sie auch eine wichtige praktische Anwendung des Themas: Untersuchung eines Systems linearer Gleichungen auf Kompatibilität.
Welchen Rang hat eine Matrix?
Die humorvolle Epigraphik des Artikels enthält viel Wahrheit. Das Wort „Rang“ selbst wird normalerweise mit einer Art Hierarchie in Verbindung gebracht, meistens mit der Karriereleiter. Je mehr Wissen, Erfahrung, Fähigkeiten, Verbindungen etc. eine Person hat. - je höher seine Position und sein Angebot an Möglichkeiten. In Jugendbegriffen bezieht sich der Rang auf den Gesamtgrad der "Härte".
Und unsere mathematischen Brüder leben nach denselben Prinzipien. Gehen wir ein paar willkürlich spazieren Nullmatrizen:
Denken wir, wenn in der Matrix nur Nullen, über welchen Rang können wir dann sprechen? Jeder kennt den umgangssprachlichen Ausdruck „Total Zero“. In der Matrixgesellschaft ist alles genau gleich:
Matrixrang Nulljede Größe ist Null.
Notiz : Die Nullmatrix wird mit dem griechischen Buchstaben "theta" bezeichnet
Um den Rang der Matrix besser zu verstehen, werde ich im Folgenden auf die Materialien zurückgreifen Analytische Geometrie. Betrachten Sie Null Vektor unseres dreidimensionalen Raumes, der keine bestimmte Richtung vorgibt und zum Bauen unbrauchbar ist affine Basis. Aus algebraischer Sicht werden die Koordinaten eines gegebenen Vektors eingeschrieben Matrix"eins nach drei" und logisch (im angegebenen geometrischen Sinne) nehmen Sie an, dass der Rang dieser Matrix Null ist.
Schauen wir uns nun einige an nicht null Spaltenvektoren Und Zeilenvektoren:
Jede Instanz hat mindestens ein Nicht-Null-Element, und das ist etwas!
Der Rang jedes Nicht-Null-Zeilenvektors (Spaltenvektors) ist gleich eins
Und überhaupt - wenn in Matrix beliebige Größen mindestens ein Element ungleich Null hat, dann seinen Rang nicht weniger Einheiten.
Algebraische Zeilen- und Spaltenvektoren sind bis zu einem gewissen Grad abstrakt, wenden wir uns also wieder der geometrischen Assoziation zu. ungleich Null Vektor gibt eine klar definierte Richtung im Raum vor und eignet sich zum Bauen Basis, also wird angenommen, dass der Rang der Matrix gleich eins ist.
Theoretischer Bezug : v Lineare Algebra ein Vektor ist ein Element eines Vektorraums (definiert durch 8 Axiome), der insbesondere eine geordnete Reihe (oder Spalte) von reellen Zahlen mit den dafür definierten Operationen Addition und Multiplikation mit einer reellen Zahl sein kann. Weitere Informationen zu Vektoren finden Sie im Artikel Lineare Transformationen.
linear abhängig(durcheinander ausgedrückt). Aus geometrischer Sicht enthält die zweite Zeile die Koordinaten des kollinearen Vektors 
, was die Sache beim Bauen nicht vorangebracht hat dreidimensionale Basis, in diesem Sinne überflüssig. Somit ist auch der Rang dieser Matrix gleich eins.
Wir schreiben die Koordinaten der Vektoren in Spalten um ( die Matrix transponieren):
Was hat sich in Bezug auf den Rang geändert? Nichts. Die Spalten sind proportional, was bedeutet, dass der Rang gleich eins ist. Beachten Sie übrigens, dass alle drei Linien auch proportional sind. Sie können mit den Koordinaten identifiziert werden drei kollineare Vektoren der Ebene, von denen nur einer nützlich, um eine "flache" Basis zu konstruieren. Und dies entspricht voll und ganz unserem geometrischen Ranggefühl.
Eine wichtige Aussage folgt aus obigem Beispiel:
Matrix Rang nach Zeilen Rang gleich Matrizen nach Spalten. Ich habe dies bereits ein wenig in der Lektion über die Effektivität erwähnt Methoden zur Berechnung der Determinante.
Notiz : Lineare Abhängigkeit von Zeilen führt zu linearer Abhängigkeit von Spalten (und umgekehrt). Aber um Zeit zu sparen und aus Gewohnheit werde ich fast immer über die lineare Abhängigkeit von Strings sprechen.
Lasst uns weiter unser geliebtes Haustier trainieren. Fügen Sie die Koordinaten eines weiteren kollinearen Vektors zur Matrix in der dritten Zeile hinzu 
:
Hat er uns beim Aufbau einer dreidimensionalen Basis geholfen? Natürlich nicht. Alle drei Vektoren gehen auf demselben Weg hin und her, und der Rang der Matrix ist Knochen. Sie können beliebig viele kollineare Vektoren nehmen, sagen wir 100, ihre Koordinaten in eine 100-mal-3-Matrix einfügen, und der Rang eines solchen Wolkenkratzers bleibt immer noch eins.
Machen wir uns mit der Matrix vertraut, deren Zeilen linear unabhängig. Zur Konstruktion einer dreidimensionalen Basis eignet sich ein Paar nicht kollinearer Vektoren. Der Rang dieser Matrix ist zwei.
Welchen Rang hat die Matrix? Die Linien scheinen nicht proportional zu sein ... also theoretisch drei. Der Rang dieser Matrix ist jedoch auch gleich zwei. Ich habe die ersten beiden Zeilen addiert und unten das Ergebnis notiert, d.h. linear ausgedrückt dritte Zeile durch die ersten beiden. Geometrisch entsprechen die Zeilen der Matrix den Koordinaten von drei koplanare Vektoren, und unter diesem Tripel gibt es ein Paar nicht-kollinearer Kameraden.
Wie du sehen kannst lineare Abhängigkeit in der betrachteten Matrix ist nicht offensichtlich, und heute werden wir nur lernen, wie man es „zu sauberem Wasser“ bringt.
Ich denke, viele Leute erraten, was der Rang einer Matrix ist!
Betrachten Sie eine Matrix, deren Zeilen linear unabhängig. Vektoren bilden affine Basis, und der Rang dieser Matrix ist drei.
Wie Sie wissen, wird jeder vierte, fünfte, zehnte Vektor des dreidimensionalen Raums linear durch Basisvektoren ausgedrückt. Wenn also eine beliebige Anzahl von Zeilen zur Matrix hinzugefügt wird, dann deren Rang werden immer noch drei sein.
Eine ähnliche Überlegung kann für Matrizen größerer Größe (offensichtlich bereits ohne geometrische Bedeutung) durchgeführt werden.
Definition : Matrixrang ist die maximale Anzahl linear unabhängiger Zeilen. Oder: Der Rang einer Matrix ist die maximale Anzahl linear unabhängiger Spalten. Ja, sie passen immer zusammen.
Aus dem oben Gesagten folgt eine wichtige praktische Richtlinie: Der Rang einer Matrix überschreitet nicht ihre Mindestdimension. Zum Beispiel in der Matrix 
vier Zeilen und fünf Spalten. Die Mindestdimension ist vier, daher wird der Rang dieser Matrix 4 sicherlich nicht überschreiten.
Notation: In der Welttheorie und -praxis gibt es keinen allgemein akzeptierten Standard für die Bezeichnung des Rangs der Matrix, der häufigste ist zu finden: - wie sie sagen, ein Engländer schreibt das eine, ein Deutscher das andere. Lassen Sie uns daher, basierend auf der bekannten Anekdote über die amerikanische und russische Hölle, den Rang der Matrix mit einem einheimischen Wort bezeichnen. Zum Beispiel: . Und wenn die Matrix "namenlos" ist, von denen es viele gibt, können Sie einfach schreiben .
Wie finde ich den Rang einer Matrix mit Minderjährigen?
Wenn unsere Großmutter eine fünfte Spalte in der Matrix hatte, dann hätte ein weiteres Moll 4. Ordnung („blau“, „Himbeere“ + 5. Spalte) berechnet werden müssen.
Abschluss: Die maximale Ordnung eines Molls ungleich Null ist drei, also .
Vielleicht hat nicht jeder diesen Satz vollständig verstanden: Der Moll 4. Ordnung ist gleich Null, aber unter den Moll 3. Ordnung gab es einen von Null verschiedenen - daher die maximale Ordnung nicht null kleiner und gleich drei.
Es stellt sich die Frage, warum nicht gleich die Determinante berechnen? Nun, erstens ist die Matrix bei den meisten Aufgaben nicht quadratisch, und zweitens wird die Aufgabe, selbst wenn Sie einen Wert ungleich Null erhalten, mit hoher Wahrscheinlichkeit abgelehnt, da dies normalerweise ein Standard-„Bottom-up“ impliziert. Lösung. Und im betrachteten Beispiel erlaubt uns die Nulldeterminante 4. Ordnung sogar zu behaupten, dass der Rang der Matrix nur kleiner als vier ist.
Ich muss zugeben, dass ich selbst auf das analysierte Problem gekommen bin, um die Methode der Eingrenzung von Minderjährigen besser zu erklären. In der Praxis ist alles einfacher:
Beispiel 2
Ermitteln Sie den Rang einer Matrix mit der Methode des Einsäumens von Minoren 
Lösung und Antwort am Ende der Lektion.
Wann läuft der Algorithmus am schnellsten? Gehen wir zurück zu derselben Vier-mal-Vier-Matrix 
. Offensichtlich ist die Lösung bei "gut" die kürzeste Ecke Minderjährige: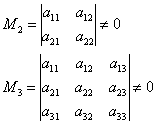
Und wenn , dann , sonst - .
Dabei ist das Denken überhaupt nicht hypothetisch – es gibt viele Beispiele, wo sich das Ganze nur auf kantige Minderjährige beschränkt.
In einigen Fällen ist jedoch eine andere Methode effektiver und vorzuziehen:
Wie findet man den Rang einer Matrix mit der Gauß-Methode?
Dieser Abschnitt richtet sich an Leser, die bereits damit vertraut sind Gauss-Methode und nach und nach bekamen sie es in die Hände.
Aus technischer Sicht ist die Methode nicht neu:
1) Mit elementaren Transformationen bringen wir die Matrix in eine Stufenform;
2) Der Rang der Matrix ist gleich der Anzahl der Zeilen.
Das ist ganz klar Die Verwendung der Gauß-Methode ändert den Rang der Matrix nicht, und das Wesentliche hier ist äußerst einfach: Gemäß dem Algorithmus werden im Zuge elementarer Transformationen alle unnötigen proportionalen (linear abhängigen) Linien identifiziert und entfernt, wodurch ein „Trockenrückstand“ verbleibt - die maximale Anzahl von linear unabhängige Linien.
Lassen Sie uns die altbekannte Matrix mit den Koordinaten von drei kollinearen Vektoren transformieren: 
(1) Die erste Reihe wurde zur zweiten Reihe addiert, multipliziert mit -2. Die erste Zeile wurde der dritten Zeile hinzugefügt.
(2) Nulllinien werden gelöscht.
Es bleibt also eine Zeile übrig, also . Das geht natürlich viel schneller, als neun Nullminoren 2. Ordnung zu berechnen und erst dann eine Schlussfolgerung zu ziehen.
Ich erinnere Sie daran algebraische Matrix nichts kann geändert werden, und Transformationen werden nur zum Zweck der Ermittlung des Ranges durchgeführt! Lassen Sie uns übrigens noch einmal auf die Frage eingehen, warum nicht? Quellmatrix 
trägt Informationen, die sich grundlegend von Matrix- und Zeileninformationen unterscheiden. In einigen mathematischen Modellen (ohne Übertreibung) kann der Unterschied in einer Zahl eine Frage von Leben und Tod sein. ...Fiel ein Schullehrer Mathematiker der Grund- und Sekundarstufe, die bei der kleinsten Ungenauigkeit oder Abweichung vom Algorithmus die Note rücksichtslos um 1-2 Punkte abschneiden. Und es war furchtbar enttäuschend, als es statt der scheinbar garantierten „fünf“ ein „gut“ oder noch schlechter herauskam. Das Verständnis kam viel später - wie sonst kann man einer Person Satelliten, Atomsprengköpfe und Kraftwerke anvertrauen? Aber keine Sorge, ich arbeite nicht in diesen Bereichen =)
Kommen wir zu sinnvolleren Aufgaben, bei denen wir uns unter anderem mit wichtigen Rechentechniken vertraut machen Gauss-Methode:
Beispiel 3
Finden Sie den Rang einer Matrix mit elementaren Transformationen 
Lösung: bei einer Vier-mal-Fünf-Matrix, was bedeutet, dass ihr Rang sicherlich nicht mehr als 4 ist.
In der ersten Spalte gibt es keine 1 oder -1, daher sind zusätzliche Schritte erforderlich, um mindestens eine Einheit zu erhalten. Während der gesamten Existenz der Site wurde mir immer wieder die Frage gestellt: „Ist es möglich, die Spalten bei elementaren Transformationen neu anzuordnen?“. Hier - die erste oder zweite Spalte neu angeordnet, und alles ist in Ordnung! Bei den meisten Aufgaben wo Gauss-Methode, Spalten können wirklich neu angeordnet werden. ABER NICHT. Und der Punkt ist nicht einmal eine mögliche Verwechslung mit Variablen, der Punkt ist, dass im klassischen Unterricht höherer Mathematik diese Aktion traditionell nicht berücksichtigt wird, daher wird ein solcher Knicks SEHR schief betrachtet (oder sogar gezwungen, alles zu wiederholen) .
Der zweite Punkt betrifft Zahlen. Im Zuge der Entscheidung ist es sinnvoll, sich an folgender Faustregel zu orientieren: elementare Transformationen sollten möglichst die Zahlen der Matrix reduzieren. Tatsächlich ist es viel einfacher, mit einer Eins-Zwei-Drei zu arbeiten als beispielsweise mit 23, 45 und 97. Und die erste Aktion zielt nicht nur darauf ab, eine Einheit in der ersten Spalte zu erhalten, sondern auch darauf, die Zahlen zu eliminieren 7 und 11.
Anfangs komplette Lösung, kommentiert dann: 
(1) Die erste Reihe wurde zur zweiten Reihe addiert, multipliziert mit -2. Die erste Zeile wurde zur dritten Zeile addiert, multipliziert mit -3. Und zum Haufen: Die 1. Zeile, multipliziert mit -1, wurde zur 4. Zeile hinzugefügt.
(2) Die letzten drei Zeilen sind proportional. Die 3. und 4. Zeile wurden gelöscht, die zweite Zeile wurde an die erste Stelle verschoben.
(3) Die erste Reihe wurde zur zweiten Reihe addiert, multipliziert mit -3.
Die auf eine Stufenform reduzierte Matrix hat zwei Reihen.
Antworten:
Jetzt sind Sie an der Reihe, die Vier-mal-Vier-Matrix zu quälen:
Beispiel 4
Finde den Rang einer Matrix mit der Gaußschen Methode 
Daran erinnere ich Sie Gauss-Methode bedeutet keine eindeutige Starrheit, und Ihre Lösung wird sich höchstwahrscheinlich von meiner Lösung unterscheiden. Ein kurzes Beispiel der Aufgabe am Ende der Lektion.
Welche Methode soll verwendet werden, um den Rang einer Matrix zu ermitteln?
In der Praxis wird oft gar nicht gesagt, mit welcher Methode der Rang ermittelt werden soll. In einer solchen Situation sollte man die Bedingung analysieren - für einige Matrizen ist es rationaler, die Lösung durch Minderjährige durchzuführen, während es für andere viel rentabler ist, elementare Transformationen anzuwenden:
Beispiel 5
Finde den Rang einer Matrix 
Lösung: der erste Weg verschwindet irgendwie sofort =)
Etwas höher habe ich geraten, die Spalten der Matrix nicht zu berühren, aber wenn es eine Nullspalte oder proportionale / übereinstimmende Spalten gibt, lohnt es sich immer noch, sie zu amputieren: 
(1) Die fünfte Spalte ist Null, wir entfernen sie aus der Matrix. Somit ist der Rang der Matrix höchstens vier. Die erste Zeile wird mit -1 multipliziert. Dies ist ein weiteres charakteristisches Merkmal der Gaußschen Methode, das die folgende Aktion zu einem angenehmen Spaziergang macht:
(2) Zu allen Zeilen, beginnend mit der zweiten, wurde die erste Zeile hinzugefügt.
(3) Die erste Reihe wurde mit -1 multipliziert, die dritte Reihe wurde durch 2 geteilt, die vierte Reihe wurde durch 3 geteilt. Die zweite Reihe, multipliziert mit -1, wurde zur fünften Reihe addiert.
(4) Die dritte Zeile wurde zur fünften Zeile hinzugefügt, multipliziert mit -2.
(5) Die letzten beiden Zeilen sind proportional, wir streichen die fünfte.
Das Ergebnis sind 4 Zeilen.
Antworten:
Fünfstöckiges Standardgebäude zur Selbsterkundung:
Beispiel 6
Finde den Rang einer Matrix
Kurze Lösung und Antwort am Ende der Lektion.
Zu beachten ist, dass der Ausdruck „Matrixrang“ in der Praxis nicht so verbreitet ist und man bei den meisten Problemen darauf verzichten kann. Aber es gibt eine Aufgabe, bei der das betrachtete Konzept die Hauptfigur ist, und am Ende des Artikels werden wir diese praktische Anwendung betrachten:
Wie untersucht man das lineare Gleichungssystem auf Kompatibilität?
Oft zusätzlich zur Lösung Systeme linearer Gleichungen je nach Bedingung ist diese zunächst auf Kompatibilität zu prüfen, also nachzuweisen, dass es überhaupt eine Lösung gibt. Eine Schlüsselrolle bei dieser Überprüfung spielt die Satz von Kronecker-Capelli, die ich in der erforderlichen Form formulieren werde:
Wenn Rang Systemmatrizen Rang gleich Erweitertes Matrixsystem, dann ist das System konsistent, und wenn die gegebene Zahl mit der Zahl der Unbekannten übereinstimmt, dann ist die Lösung eindeutig.
Um das System auf Kompatibilität zu untersuchen, ist es daher notwendig, die Gleichheit zu überprüfen 
, Wo - Systemmatrix(Denken Sie an die Terminologie aus der Lektion Gauss-Methode), A - Erweitertes Matrixsystem(d.h. Matrix mit Koeffizienten bei Variablen + Spalte freier Terme).
Zeilen (Spalten). Mehrere Zeilen (Spalten) heißen linear unabhängig, wenn keine davon linear durch andere ausgedrückt werden kann. Der Rang des Zeilensystems ist immer gleich dem Rang des Spaltensystems, und diese Zahl wird Rang der Matrix genannt.
Der Rang einer Matrix ist die höchste der Ordnungen aller möglichen von Null verschiedenen Unterwerte dieser Matrix. Der Rang einer Nullmatrix beliebiger Größe ist Null. Wenn alle Minderjährigen zweiter Ordnung gleich Null sind, dann ist der Rang gleich Eins und so weiter.
Matrixrang - Bilddimension dim (im (A)) (\displaystyle \dim(\operatorname (im) (A))) linear operator , der der Matrix entspricht.
Normalerweise der Rang der Matrix A (\displaystyle A) bezeichnet Rang A (\displaystyle \operatorname (rang) A), r EIN (\displaystyle \operatorname (r) EIN), rg A (\displaystyle \operatorname (rg)A) oder Rang A (\displaystyle \operatorname (Rang) A). Die letzte Option ist für auf Englisch, während die ersten beiden für Deutsch, Französisch und eine Reihe anderer Sprachen sind.
Enzyklopädisches YouTube
-
1 / 5
Sei eine rechteckige Matrix.
Dann per Definition der Rang der Matrix A (\displaystyle A) Ist:
Satz (über die Richtigkeit der Definition von Rängen). Lassen Sie alle Matrix Minoren A m × n (\displaystyle A_(m\times n)) Befehl k (\ displaystyle k) sind gleich Null ( Mk = 0 (\displaystyle M_(k)=0)). Dann ∀ M k + 1 = 0 (\displaystyle \forall M_(k+1)=0) wenn sie existieren.
Verwandte Definitionen
Eigenschaften
- Satz (auf Basis Minor): Lassen r = klingelte A , M r (\displaystyle r=\operatorname (rang) A,M_(r))- Basis-Moll der Matrix A (\displaystyle A), Dann:
- Folgen:
- Satz (über Ranginvarianz unter elementaren Transformationen): Führen wir eine Notation für Matrizen ein, die durch elementare Transformationen voneinander erhalten werden. Dann ist die Aussage wahr: Wenn A ∼ B (\displaystyle A\sim B), dann sind ihre Reihen gleich.
- Satz Kronecker - Cappelli: Ein System linearer algebraischer Gleichungen ist genau dann konsistent, wenn der Rang seiner Hauptmatrix gleich dem Rang seiner erweiterten Matrix ist. Insbesondere:
- Die Anzahl der Hauptvariablen des Systems ist gleich dem Rang des Systems.
- Ein konsistentes System ist definiert (seine Lösung ist eindeutig), wenn der Rang des Systems gleich der Anzahl aller seiner Variablen ist.
- Ungleichheit Sylvester : Wenn A Und B Größenmatrizen m x n Und n x k, Das
Dies ist ein Spezialfall der folgenden Ungleichung.
- Ungleichung Frobenius : Wenn AB, BC, ABC wohldefiniert sind, dann
Lineare Transformation und Matrixrang
Lassen A (\displaystyle A)- Größenmatrix m × n (\displaystyle m\times n)über das Feld C (\displaystyle C)(oder R (\displaystyle R)). Lassen T (\displaystyle T) ist eine lineare Transformation entsprechend A (\displaystyle A) in der Standardbasis; es bedeutet das T (x) = A x (\displaystyle T(x)=Ax). Matrix-Rang A (\displaystyle A) ist die Dimension des Transformationsbereichs T (\displaystyle T).
Methoden
Es gibt mehrere Methoden, um den Rang einer Matrix zu ermitteln:
- Methode der elementaren Transformationen
- Fransen-Minor-Methode
Jede Matrix A Befehl m×n kann als Sammlung angesehen werden M Zeilenvektoren bzw N Spaltenvektoren .
Rang Matrizen A Befehl m×n die maximale Anzahl von linear unabhängigen Spaltenvektoren oder Zeilenvektoren ist.
Wenn der Rang der Matrix A gleich R, dann steht geschrieben:
Ermitteln des Rangs einer Matrix
Lassen A beliebige Ordnungsmatrix M× N. Den Rang einer Matrix finden A wenden Sie das Gaußsche Eliminationsverfahren darauf an.
Beachten Sie, dass, wenn sich herausstellt, dass das führende Element zu einem bestimmten Zeitpunkt der Eliminierung gleich Null ist, wir diese Zeichenfolge durch eine Zeichenfolge ersetzen, in der das führende Element von Null verschieden ist. Wenn sich herausstellt, dass es keine solche Zeile gibt, gehen wir zur nächsten Spalte und so weiter.
Nach der Vorwärtsbewegung der Gaußschen Elimination erhalten wir eine Matrix, deren Elemente unter der Hauptdiagonale gleich Null sind. Außerdem kann es Nullzeilenvektoren geben.
Die Anzahl der Nicht-Null-Zeilenvektoren ist der Rang der Matrix A.
Sehen wir uns das alles anhand einfacher Beispiele an.
Beispiel 1
Multiplizieren der ersten Reihe mit 4 und Addieren zur zweiten Reihe und Multiplizieren der ersten Reihe mit 2 und Addieren zur dritten Reihe haben wir:
Multiplizieren Sie die zweite Zeile mit -1 und addieren Sie sie zur dritten Zeile:
Wir haben zwei Nicht-Null-Zeilen und daher ist der Rang der Matrix 2.
Beispiel 2
Finden Sie den Rang der folgenden Matrix:
Multipliziere die erste Zeile mit -2 und addiere zur zweiten Zeile. Setzen Sie auf ähnliche Weise die Elemente der dritten und vierten Zeile der ersten Spalte auf Null:
Setzen wir die Elemente der dritten und vierten Zeile der zweiten Spalte zurück, indem wir die entsprechenden Zeilen zur zweiten Zeile addieren, multipliziert mit der Zahl -1.
In diesem Artikel werden ein solches Konzept wie der Rang einer Matrix und die notwendigen zusätzlichen Konzepte erörtert. Wir geben Beispiele und Beweise für das Ermitteln des Rangs einer Matrix und sagen Ihnen auch, was ein Matrix-Minor ist und warum er so wichtig ist.
Matrix-Moll
Um zu verstehen, was der Rang einer Matrix ist, ist es notwendig, ein solches Konzept als Matrix-Minor zu verstehen.
Bestimmung 1
UnerheblichkMatrix ter Ordnung - die Determinante einer quadratischen Matrix der Ordnung k × k, die sich aus den Elementen der Matrix A zusammensetzt, die sich in vorgewählten k-Zeilen und k-Spalten befinden, wobei die Position der Elemente der Matrix A beibehalten wird.
Einfach ausgedrückt, wenn wir in Matrix A (p-k) Zeilen und (n-k) Spalten löschen und aus den verbleibenden Elementen eine Matrix erstellen, wobei wir die Anordnung der Elemente von Matrix A beibehalten, dann ist die Determinante der resultierenden Matrix der Minor der Ordnung k der Matrix A.
Aus dem Beispiel folgt, dass die Minoren erster Ordnung der Matrix A die Matrixelemente selbst sind.
Wir können einige Beispiele für Minderjährige 2. Ordnung geben. Wählen wir zwei Zeilen und zwei Spalten. Zum Beispiel 1. und 2. Reihe, 3. und 4. Spalte.
Mit dieser Wahl der Elemente wird der Moll zweiter Ordnung - 1 3 0 2 = (- 1) × 2 - 3 × 0 = - 2 sein
Ein weiterer Minor zweiter Ordnung der Matrix A ist 0 0 1 1 = 0
Lassen Sie uns die Konstruktion von Minoren zweiter Ordnung der Matrix A veranschaulichen:
Den Minor 3. Ordnung erhält man durch Streichen der dritten Spalte der Matrix A:
0 0 3 1 1 2 - 1 - 4 0 = 0 × 1 × 0 + 0 × 2 × (- 1) + 3 × 1 × (- 4) - 3 × 1 × (- 1) - 0 × 1 × 0 - 0 × 2 × (- 4) = - 9
Eine Veranschaulichung, wie der Minor 3. Ordnung der Matrix A erhalten wird:
Für eine gegebene Matrix gibt es keine Mollzahlen höher als die 3. Ordnung, weil
k ≤ m ich n (p , n) = m ich n (3 , 4) = 3
Wie viele Minoren k-ter Ordnung gibt es für eine Matrix A der Ordnung p×n?
Die Anzahl der Minderjährigen errechnet sich nach folgender Formel:
C p k × C n k , g e C p k = p ! k! (p - k) ! und C nk = n ! k! (n - k) ! - die Anzahl der Kombinationen von p bis k bzw. von n bis k.
Nachdem wir entschieden haben, was die Minoren der Matrix A sind, können wir mit der Bestimmung des Rangs der Matrix A fortfahren.
Matrix-Rang: Methoden des Findens
Bestimmung 2Matrix-Rang - die höchste Ordnung der Matrix, außer Null.
Bezeichnung 1
Rang (A), Rg(A), Rang(A).
Aus der Definition des Rangs einer Matrix und des Minors einer Matrix wird deutlich, dass der Rang einer Nullmatrix gleich Null ist und der Rang einer Nicht-Null-Matrix von Null verschieden ist.
Definition des Rangs einer Matrix
Bestimmung 3Kleinere Aufzählungsmethode - ein Verfahren, das auf der Bestimmung des Rangs einer Matrix basiert.
Aktionsalgorithmus durch Aufzählung von Minderjährigen :
Es ist notwendig, den Rang der Ordnungsmatrix A zu finden P× N. Wenn es mindestens ein Element ungleich Null gibt, ist der Rang der Matrix mindestens gleich eins ( Weil ist ein Moll 1. Ordnung, der ungleich Null ist).
Dann folgt die Aufzählung der Minderjährigen 2. Ordnung. Wenn alle Minderjährigen 2. Ordnung gleich Null sind, dann ist der Rang gleich Eins. Wenn mindestens ein Minor 2. Ordnung ungleich Null vorhanden ist, muss zur Aufzählung der Minoren 3. Ordnung übergegangen werden, und der Rang der Matrix beträgt in diesem Fall mindestens zwei.
Machen wir dasselbe mit dem Rang 3. Ordnung: Wenn alle Minoren der Matrix gleich Null sind, dann ist der Rang gleich zwei. Wenn es mindestens einen Minor dritter Ordnung ungleich Null gibt, ist der Rang der Matrix mindestens drei. Und so weiter, analog.
Beispiel 2
Finde den Rang einer Matrix:
A \u003d - 1 1 - 1 - 2 0 2 2 6 0 - 4 4 3 11 1 - 7
Da die Matrix nicht Null ist, ist ihr Rang mindestens gleich eins.
Der Minor 2. Ordnung - 1 1 2 2 = (- 1) × 2 - 1 × 2 = 4 ist ungleich Null. Dies impliziert, dass der Rang der Matrix A mindestens zwei ist.
Wir sortieren die Minderjährigen der 3. Ordnung: C 3 3 × C 5 3 \u003d 1 5 ! 3! (5 - 3) ! = 10 Stück.
1 1 - 1 2 2 6 4 3 11 = (- 1) × 2 × 11 + 1 × 6 × 4 + (- 1) × 2 × 3 - (- 1) × 2 × 4 - 1 × 2 × 11 - (-1) × 6 × 3 = 0
1 - 1 - 2 2 6 0 4 11 1 = (- 1) × 6 × 1 + (- 1) × 0 × 4 + (- 2) × 2 × 11 - (- 2) × 6 × 4 - (- 1) × 2 × 1 – (- 1) × 0 × 11 = 0
1 1 - 2 2 2 0 4 3 1 = (- 1) × 2 × 1 + 1 × 0 × 4 + (- 2) × 2 × 3 - (- 2) × 2 × 4 - 1 × 2 × 1 - (-1) × 0 × 3 = 0
1 - 1 0 2 6 - 4 4 11 - 7 = (- 1) × 6 × (- 7) + (- 1) × (- 4) × 4 + 0 × 2 × 11 - 0 × 6 × 4 - ( - 1) × 2 × (- 7) - (- 1) × (- 4) × 11 = 0
1 - 1 0 2 6 - 4 3 11 - 7 = 1 × 6 × (- 7) + (- 1) × (- 4) × 3 + 0 × 2 × 11 - 0 × 6 × 3 - (- 1) × 2 × (– 7) – 1 × (– 4) × 11 = 0
1 - 2 0 2 0 - 4 3 1 - 7 = 1 × 0 × (- 7) + (- 2) × (- 4) × 3 + 0 × 2 × 1 - 0 × 0 × 3 - (- 2) × 2 × (- 7) – 1 × (- 4) × 1 = 0
1 - 2 0 6 0 - 4 11 1 - 7 = (- 1) × 0 × (- 7) + (- 2) × (- 4) × 11 + 0 × 6 × 1 - 0 × 0 × 11 - ( - 2) × 6 × (- 7) - (- 1) × (- 4) × 1 = 0
Die Minderjährigen 3. Ordnung sind null, also ist der Rang der Matrix zwei.
Antworten : Rang (A) = 2.
Ermitteln des Rangs einer Matrix mit der Methode des Einsäumens von Minoren
Bestimmung 3Fransen-Minor-Methode - eine Methode, mit der Sie mit weniger Rechenaufwand ein Ergebnis erzielen können.
Fransen Moll - Minor M o k (k + 1) --te Ordnung der Matrix A, die an die Minor M der Ordnung k der Matrix A grenzt, wenn die Matrix, die der Minor M o k entspricht, die Matrix "enthält", die der Minor entspricht M.
Einfach ausgedrückt wird die dem umrandeten Moll M entsprechende Matrix aus der dem umrandenden Moll M o k entsprechenden Matrix erhalten, indem die Elemente einer Zeile und einer Spalte gelöscht werden.
Beispiel 3
Finde den Rang einer Matrix:
A = 1 2 0 - 1 3 - 2 0 3 7 1 3 4 - 2 1 1 0 0 3 6 5
Um den Rang zu finden, nehmen wir den Moll 2. Ordnung M = 2 - 1 4 1
Wir schreiben alle angrenzenden Minderjährigen auf:
1 2 - 1 - 2 0 7 3 4 1 , 2 0 - 1 0 3 7 4 - 2 1 , 2 - 1 3 0 7 1 4 1 1 , 1 2 - 1 3 4 1 0 0 6 , 2 0 - 1 4 - 2 1 0 3 6 , 2 - 1 3 4 1 1 0 6 5 .
Um die Methode der Eingrenzung von Minderjährigen zu untermauern, stellen wir einen Satz vor, dessen Formulierung keine Beweisbasis erfordert.
Satz 1
Wenn alle Minoren, die an den Minor k-ter Ordnung einer Matrix A der Ordnung p mal n grenzen, gleich Null sind, dann sind alle Minoren der Ordnung (k + 1) der Matrix A gleich Null.
Aktionsalgorithmus :
Um den Rang einer Matrix zu finden, ist es nicht notwendig, alle Minoren durchzugehen, sondern nur die Grenzen zu betrachten.
Wenn die angrenzenden Minderjährigen gleich Null sind, dann ist der Rang der Matrix Null. Existiert mindestens ein Minor ungleich Null, dann betrachten wir angrenzende Minoren.
Wenn sie alle null sind, dann ist Rang(A) zwei. Wenn es mindestens einen angrenzenden Minor ungleich Null gibt, fahren wir fort, seine angrenzenden Minors zu betrachten. Und so weiter, in ähnlicher Weise.
Beispiel 4
Ermitteln Sie den Rang einer Matrix mit der Methode des Einsäumens von Minoren
A = 2 1 0 - 1 3 4 2 1 0 - 1 2 1 1 1 - 4 0 0 2 4 - 14
Wie entscheiden?
Da das Element a 11 der Matrix A ungleich Null ist, nehmen wir den Moll 1. Ordnung. Beginnen wir mit der Suche nach einem angrenzenden Moll außer Null:
2 1 4 2 = 2 x 2 - 1 x 4 = 0 2 0 4 1 = 2 x 1 - 0 x 4 = 2
Wir haben einen angrenzenden Moll 2. Ordnung gefunden, der ungleich Null 2 0 4 1 ist.
Lassen Sie uns die angrenzenden Untertöne aufzählen - (es gibt (4 - 2) × (5 - 2) = 6 Stücke).
2 1 0 4 2 1 2 1 1 = 0 ; 2 0 - 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 - 1 2 1 - 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 - 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 - 1 0 2 - 14 = 0
Antworten : Rang(A) = 2.
Ermitteln des Rangs einer Matrix nach der Gauß-Methode (unter Verwendung elementarer Transformationen)
Erinnern Sie sich, was elementare Transformationen sind.
Elementare Transformationen:
- durch Umordnen der Zeilen (Spalten) der Matrix;
- durch Multiplizieren aller Elemente einer beliebigen Reihe (Spalte) der Matrix mit einer beliebigen Nicht-Null-Zahl k;
durch Hinzufügen von Elementen zu den Elementen einer beliebigen Zeile (Spalte), die einer anderen Zeile (Spalte) der Matrix entsprechen, die mit einer beliebigen Zahl k multipliziert werden.
Bestimmung 5
Ermitteln des Rangs einer Matrix mit der Gauß-Methode - ein Verfahren, das auf der Theorie der Matrixäquivalenz basiert: Wenn Matrix B aus Matrix A unter Verwendung einer endlichen Anzahl elementarer Transformationen erhalten wird, dann ist Rank(A) = Rank(B).
Die Gültigkeit dieser Aussage folgt aus der Definition der Matrix:
- bei einer Permutation der Zeilen oder Spalten einer Matrix wechselt deren Determinante das Vorzeichen. Wenn es gleich Null ist, dann bleibt es beim Permutieren von Zeilen oder Spalten gleich Null;
- im Fall der Multiplikation aller Elemente einer beliebigen Zeile (Spalte) der Matrix mit einer beliebigen Zahl k, die ungleich Null ist, ist die Determinante der resultierenden Matrix gleich der Determinante der ursprünglichen Matrix, die multipliziert wird von k;
im Fall der Addition der Elemente einer bestimmten Reihe oder Spalte der Matrix die entsprechenden Elemente einer anderen Reihe oder Spalte, die mit der Zahl k multipliziert werden, ändert ihre Determinante nicht.
Das Wesen der Methode der elementaren Transformationen : die Matrix, deren Rang ermittelt werden soll, durch elementare Transformationen auf eine trapezförmige reduzieren.
Wofür?
Der Rang von Matrizen dieser Art ist recht einfach zu finden. Es ist gleich der Anzahl der Zeilen, die mindestens ein Nicht-Null-Element enthalten. Und da sich der Rang bei elementaren Transformationen nicht ändert, ist dies der Rang der Matrix.
Lassen Sie uns diesen Prozess veranschaulichen:
- für rechteckige Matrizen A der Ordnung p mal n, deren Zeilenzahl größer ist als die Spaltenzahl:
A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 n 0 0 0 ⋯ 0 1 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 , R. ein n k (A) = n
A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R ein n k (A) = k
- für rechteckige Matrizen A der Ordnung p mal n, deren Zeilenzahl kleiner ist als die Spaltenzahl:
A ~ 1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b p p + 1 ⋯ b p n , R ein n k (A) = p
A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0
- für quadratische Matrizen A der Ordnung n mal n:
A ~ 1 b 12 b 13 ⋯ b 1 n - 1 b 1 n 0 1 b 23 ⋯ b 2 n - 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n - 1 n 0 0 0 ⋯ 0 1 , R ein n k (A) = n
A ~ 1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R ein n k (A) = k , k< n
Beispiel 5
Finden Sie den Rang der Matrix A mit elementaren Transformationen:
A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11
Wie entscheiden?
Da das Element a 11 ungleich Null ist, müssen die Elemente der ersten Zeile der Matrix A mit 1 a 11 \u003d 1 2 multipliziert werden:
A = 2 1 - 2 6 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~
Wir addieren zu den Elementen der 2. Reihe die entsprechenden Elemente der 1. Reihe, die mit (-3) multipliziert werden. Zu den Elementen der 3. Reihe addieren wir die Elemente der 1. Reihe, die mit (-1) multipliziert werden:
~ A (1) \u003d 1 1 2 - 1 3 3 0 0 - 1 1 - 1 2 - 7 5 - 2 4 - 15 7 2 - 4 11 ~ A (2) \u003d \u003d 1 1 2 - 1 3 3 + 1 (- 3) 0 + 1 2 (- 3) 0 + (- 1) (- 3) - 1 + 3 (- 3) 1 + 1 (- 3) - 1 + 1 2 (- 3) 2 + (- 1) (- 1) - 7 + 3 (- 1) 5 + 1 (- 5) - 2 + 1 2 (- 5) 4 + (- 1) (- 5) - 15 + 3 (- 5 ) 7 + 1 (- 7) 2 + 1 2 (- 7) - 4 + (- 1) (- 7) 11 + 3 (- 7) =
1 1 2 - 1 3 0 - 3 2 3 - 10 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10
Das Element a 22 (2) ist ungleich Null, also multiplizieren wir die Elemente der 2. Zeile der Matrix A mit A (2) mit a 1 a 22 (2) = - 2 3:
A (3) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 3 - 10 0 - 9 2 9 - 30 0 - 3 2 3 - 10 ~ A (4) \u003d 1 1 2 - 1 3 0 1 - 2 20 3 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 0 - 9 2 + 1 9 2 9 + (- 2) 9 2 - 30 + 20 3 × 9 2 0 - 3 2 + 1 3 2 3 + (- 2) 3 2 - 10 + 20 3 × 3 2 = = 1 1 2 - 1 3 0 1 - 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0
- Zu den Elementen der 3. Reihe der resultierenden Matrix addieren wir die entsprechenden Elemente der 2. Reihe, die mit 3 2 multipliziert werden;
- zu den Elementen der 4. Reihe - die Elemente der 2. Reihe, die mit 9 2 multipliziert werden;
- zu den Elementen der 5. Reihe - die Elemente der 2. Reihe, die mit 3 2 multipliziert werden.
Alle Zeilenelemente sind Null. Wir haben also mit Hilfe elementarer Transformationen die Matrix auf eine Trapezform reduziert, woraus ersichtlich ist, dass R a n k (A (4)) = 2 . Daraus folgt, dass der Rang der ursprünglichen Matrix ebenfalls gleich zwei ist.
Kommentar
Wenn Sie elementare Umformungen vornehmen, dann sind Näherungswerte nicht erlaubt!
Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Enter
Bisher für eine quadratische Matrix
Ordnung wurde der Begriff des Minderjährigen eingeführt 
Element 
. Denken Sie daran, dass dies der Name der Determinante der Reihenfolge war 
, erhalten aus der Determinante 
durchstreichen 
-te Zeile und 
-te Spalte.Lassen Sie uns jetzt vorstellen allgemeines Konzept unerheblich. Betrachten wir einige nicht unbedingt quadratisch Matrix
. Wählen wir einige aus 
Linien Nummern 
Und 
Spaltennummern 
.Definition. Kleiner Auftrag
Matrizen 
(entsprechend den ausgewählten Zeilen und Spalten) wird Ordnungsdeterminante genannt 
, gebildet durch Elemente, die am Schnittpunkt der ausgewählten Zeilen und Spalten stehen, d.h. Nummer
.Jede Matrix hat so viele Minoren einer bestimmten Ordnung
Auf wie viele Arten können Zeilennummern gewählt werden? 
und Spalten 
.Definition. In der Matrix
Größen 
Minor bestellen 
genannt Basic, wenn es von Null verschieden ist, und alle Minoren der Ordnung 
null oder kleinere Ordnungen sind 
an der Matrix 
absolut nicht.Es ist klar, dass es in einer Matrix mehrere verschiedene Basisminoren geben kann, aber alle Basisminoren die gleiche Reihenfolge haben. In der Tat, wenn alle Minderjährigen in Ordnung sind
gleich Null sind, dann sind sie gleich Null und alle Minoren der Ordnung 
, und folglich aller höheren Ordnungen.Definition. Matrix-Rang wird die Ordnung des Basis-Minors genannt, oder mit anderen Worten, die größte Ordnung, für die Minoren ungleich Null existieren. Wenn alle Elemente einer Matrix gleich Null sind, wird der Rang einer solchen Matrix per Definition als Null angesehen.
Matrix-Rang
wird durch das Symbol gekennzeichnet 
. Aus der Definition des Rangs folgt der für die Matrix 
Größen 
faires Verhältnis.Zwei Möglichkeiten, den Rang einer Matrix zu berechnen
A) Fransen-Minor-Methode
Lassen Sie den Moll in der Matrix finden
Ordnung, von Null verschieden. Betrachten Sie nur diese Minderjährigen 
-ten Ordnung, die (Surround-)Moll enthalten 
: Wenn sie alle Null sind, dann ist der Rang der Matrix 
. Andernfalls gibt es unter den angrenzenden Minoren einen von Null verschiedenen Minor 
Ordnung, und die ganze Prozedur wird wiederholt.Beispiel 9 . Finde den Rang einer Matrix
nach der Methode der angrenzenden Minderjährigen.
Wir wählen ein Moll zweiter Ordnung
. Es gibt nur einen Moll dritter Ordnung, der an den gewählten Moll grenzt 
. Rechnen wir es aus.
So gering
einfach, und der Rang der Matrix ist gleich ihrer Reihenfolge, d.h. 
Es ist klar, dass das Sortieren von Minoren auf diese Weise auf der Suche nach einer Basis eine Aufgabe ist, die mit großen Berechnungen verbunden ist, wenn die Dimensionen der Matrix nicht sehr klein sind. Es gibt jedoch einen einfacheren Weg, den Rang einer Matrix zu finden - mit elementaren Transformationen.
B) Methode der elementaren Transformationen
Definition. Elementare Matrizentransformationen nannte die folgenden Transformationen:
Multiplizieren einer Zeichenfolge mit einer Zahl ungleich Null;
Hinzufügen einer weiteren Zeile zu einer Zeile;
Linienpermutation;
dieselben Spaltentransformationen.
Die Transformationen 1 und 2 werden elementweise durchgeführt.
Durch die Kombination von Transformationen der ersten und zweiten Art können wir zu jeder beliebigen Linie eine Linearkombination der verbleibenden Linien hinzufügen.
Satz. Elementare Transformationen ändern den Rang der Matrix nicht.
(kein Beweis)
Die Idee einer praktischen Methode zur Berechnung des Rangs einer Matrix
liegt darin, dass mit Hilfe elementarer Transformationen die gegebene Matrix
zur Aussicht führen
,
(5)in denen die "diagonalen" Elemente
von Null verschieden sind und die unter den "diagonalen" liegenden Elemente gleich Null sind. Nennen wir die Matrix 
diese Art von Dreieck (andernfalls wird es Diagonale, Trapez oder Treppe genannt). Nach dem Bringen der Matrix 
in eine Dreiecksform können wir das sofort schreiben 
.Tatsächlich,
(weil elementare Transformationen den Rang nicht ändern). Aber die Matrix 
es gibt eine von Null verschiedene Ordnung 
:
,und jeder Minderjährige des Ordens
enthält den Null-String und ist daher null.Lassen Sie uns nun ein praktisches formulieren Rangberechnungsregel Matrizen
mit elementaren Transformationen: um den Rang einer Matrix zu finden 
es soll mit Hilfe elementarer Transformationen in eine Dreiecksform gebracht werden 
. Dann der Rang der Matrix 
gleich der Anzahl der Nicht-Null-Zeilen in der resultierenden Matrix 
.Beispiel 10 Finde den Rang einer Matrix
Methode der elementaren Transformationen
Lösung.
Lassen Sie uns die erste und zweite Zeile vertauschen (weil das erste Element der zweiten Zeile −1 ist und es praktisch ist, damit Transformationen durchzuführen). Als Ergebnis erhalten wir eine Matrix, die der gegebenen entspricht.
Bezeichnen
-te Zeile der Matrix – 
. Wir müssen die ursprüngliche Matrix in eine dreieckige Form bringen. Wir werden die erste Linie als die führende betrachten, sie wird an allen Transformationen teilnehmen, aber selbst bleibt unverändert.In der ersten Phase führen wir Transformationen durch, die es uns ermöglichen, Nullen in der ersten Spalte zu erhalten, mit Ausnahme des ersten Elements. Subtrahieren Sie dazu von der zweiten Reihe die erste, multipliziert mit 2
, fügen Sie die erste Zeile zur dritten Zeile hinzu 
, und von der dritten subtrahieren wir die erste, multipliziert mit 3 
Wir erhalten eine Matrix, deren Rang mit dem Rang der gegebenen Matrix übereinstimmt. Nennen wir es mit demselben Buchstaben 
:
.Da wir die Matrix auf die Form (5) bringen müssen, subtrahieren wir die zweite von der vierten Reihe. Dabei haben wir:
.Es wird eine Dreiecksmatrix erhalten, und daraus kann geschlossen werden
, d. h. die Anzahl der Nicht-Null-Zeilen. Die Lösung des Problems lässt sich kurz wie folgt schreiben:
