Mga halaga ng argumento z sa ilalim ng kung saan f(z) napupunta sa zero na tinatawag. zero point, ibig sabihin. Kung f(a) = 0 , pagkatapos a - zero point.
Def. Dot A tinawag order zeron
, Kung
Ang FKP ay maaaring katawanin sa anyo f(z) = , saan 
analytic function at 
0.
Sa kasong ito, sa pagpapalawak ng function sa isang Taylor series (43), ang una n ang mga coefficient ay zero
=
=
atbp. Tukuyin ang pagkakasunud-sunod ng zero para sa 
at (1-cos z) sa z
=
0
=
=
zero 1st order
1 - cos z
=
=
zero ika-2 order
Def. Dot z
=
tinawag ituro sa infinity At sero mga function f(z), Kung f(
) = 0. Ang ganitong function ay lumalawak sa isang serye sa mga negatibong kapangyarihan z
: f(z)
=
. Kung
una n
ang mga coefficient ay katumbas ng zero, pagkatapos ay dumating kami sa zero order n
sa isang punto sa infinity: f(z)
= z
-
n
.
Ang mga nakahiwalay na puntong isahan ay nahahati sa: a) naaalis na mga singular na puntos; b) mga poste ng ordern; V) mahahalagang iisang puntos.
Dot A tinawag naaalis na singular na punto mga function f(z) kung z 
a
lim f(z)
= kasama si - may hangganang bilang .
Dot A tinawag poste ng kaayusann
(n
1) mga tampok f(z) kung ang inverse function 
=
1/
f(z) ay may order na zero n sa punto A. Ang ganitong function ay maaaring palaging kinakatawan bilang f(z)
=
, Saan 
- analytical function at 
.
Dot A tinawag mahalagang punto mga function f(z), kung z 
a
lim f(z) ay wala.
Serye ni Laurent
Isaalang-alang ang kaso ng annular convergence region r < | z 0 – a| < R nakasentro sa isang punto A para sa function f(z). Ipinakilala namin ang dalawang bagong lupon L 1 (r) At L 2 (R) malapit sa mga hangganan ng singsing na may tuldok z 0 sa pagitan nila. Gumawa tayo ng isang seksyon ng singsing, pagsamahin ang mga bilog sa mga gilid ng seksyon, dumaan sa isang simpleng konektadong rehiyon, at sa
Cauchy integral formula (39) nakakakuha tayo ng dalawang integral sa variable na z
f(z 0)
=
+
,
(42)
kung saan napupunta ang pagsasama sa magkasalungat na direksyon.
Para sa integral over L 1 ang kundisyon | z 0 – a | > | z – a |, at para sa integral over L 2 baligtad na kondisyon | z 0 – a | < | z – a |. Samakatuwid, ang kadahilanan 1/( z – z 0) palawakin sa isang serye (a) sa integral over L 2 at sa serye (b) sa integral over L 1 . Bilang isang resulta, nakukuha namin ang agnas f(z) sa annular na rehiyon sa Serye ni Laurent sa positibo at negatibong kapangyarihan ( z 0 – a)
f(z 0)
=
A n
(z 0 – a) n
(43)
saan A n
=
=
;A -n
=
Pagpapalawak sa mga positibong kapangyarihan (z 0 - A) tinawag kanang bahagi Laurent series (Taylor series), at ang pagpapalawak sa mga negatibong kapangyarihan ay tinatawag. pangunahing bahagi Laurent row.
Kung nasa loob ng bilog L 1 walang mga singular na puntos at ang function ay analytic, pagkatapos ay sa (44) ang unang integral ay katumbas ng zero ng Cauchy theorem, at ang tamang bahagi lamang ang nananatili sa pagpapalawak ng function. Ang mga negatibong kapangyarihan sa pagpapalawak (45) ay lilitaw lamang kapag nalabag ang analyticity sa loob ng inner circle at nagsisilbing paglalarawan ng function na malapit sa mga nakahiwalay na puntong isahan.
Upang bumuo ng serye ng Laurent (45) para sa f(z) maaaring kalkulahin ang mga koepisyent ng pagpapalawak ayon sa pangkalahatang pormula o gamitin ang mga pagpapalawak ng mga elementong pag-andar na kasama sa f(z).
Bilang ng mga termino ( n) ng pangunahing bahagi ng serye ng Laurent ay depende sa uri ng singular na punto: naaalis na singular na punto
(n
=
0)
; mahalagang isahan na punto
(n 
);
posten-ika-utos(n
-
numero ng pagtatapos).
at para sa f(z)
=
tuldok z
= 0 naaalis na singular na punto, kasi walang pangunahing bahagi. f(z)
=
(z
-
) = 1 -
b) Para sa f(z)
=
tuldok z
= 0 -
1st order poste
f(z)
=
(z
-
) =
-
c) Para sa f(z) = e 1 / z tuldok z = 0 - mahalagang isahan na punto
f(z)
=
e 1 /
z =
Kung f(z) ay analytic sa domain D maliban sa m nakahiwalay na mga puntong isahan 
at | z 1 |
< |z 2 |
< . . . < |z m| , pagkatapos ay kapag pinalawak ang pag-andar sa mga kapangyarihan z ang buong eroplano ay nahahati sa m+ 1 singsing | z i |
< | z
| < | z i+ 1 | at ang serye ng Laurent ay may ibang anyo para sa bawat singsing. Kapag lumalawak ang kapangyarihan ( z
–
z i
) ang convergence region ng Laurent series ay ang circle | z
–
z i
| < r, Saan r
ay ang distansya sa pinakamalapit na singular na punto.
atbp. Palawakin ang function f(z)
=
sa serye ni Laurent sa powers z At ( z
-
1).
Solusyon. Kinakatawan namin ang function sa form f(z)
= - z 2
. Ginagamit namin ang formula para sa kabuuan ng isang geometric na pag-unlad 
. Sa bilog |z|< 1 ряд сходится и f(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . . . , ibig sabihin. decomposition naglalaman lamang tama Bahagi. Lumipat tayo sa panlabas na rehiyon ng bilog |z| > 1 . Kinakatawan namin ang function sa form 
, kung saan 1/| z|
< 1, и получим разложение f(z)
= z
=z
+ 1 +
kasi , pagpapalawak ng function sa mga kapangyarihan ( z
-
1) parang f(z)
= (z
-
1) -1
+ 2 + (z
-
1) para sa lahat 
1.
atbp. Palawakin ang function sa isang Laurent series f(z)
=
:
a) sa mga degree z sa isang bilog | z|
< 1; b)
по степеням z
singsing 1<
|z|
< 3 ; c)
по степеням (z
–
2).Desisyon. I-decompose natin ang function sa mga simpleng fraction
=
=
+
=
.
Mula sa mga kondisyon z
=1
A
= -1/2 , z
=3
B
= ½.
A) f(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], kapag | z|<
1.
b) f(z)
= - ½ [ 
+
]
= -
(
), sa 1< |z|
< 3.
kasama) f(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, para sa |2 - z|
< 1
Ito ay isang bilog ng radius 1 na nakasentro sa isang punto z = 2 .
Sa ilang mga kaso, ang serye ng kapangyarihan ay maaaring mabawasan sa isang hanay ng mga geometric na pag-unlad, at pagkatapos ay madaling matukoy ang lugar ng kanilang tagpo.
atbp. Siyasatin ang convergence ng isang serye
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Solusyon. Ito ay ang kabuuan ng dalawang geometric progression na may q 1
=
, q 2 = () . Mula sa mga kondisyon ng kanilang convergence ito ay sumusunod 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
2. Hanapin ang mga zero ng function.
f(x) sa x 
.
Sagutin ang f(x) sa x .
2) x 2 > -4x-5;
x 2 +4x +5>0;
Hayaan ang f (x) \u003d x 2 + 4 x + 5 pagkatapos ay Hanapin ang naturang x kung saan ang f (x)> 0,
D=-4 Walang mga zero.
4. Mga sistema ng hindi pagkakapantay-pantay. Mga hindi pagkakapantay-pantay at mga sistema ng hindi pagkakapantay-pantay na may dalawang variable
1) Ang hanay ng mga solusyon sa isang sistema ng hindi pagkakapantay-pantay ay ang intersection ng mga hanay ng mga solusyon ng mga hindi pagkakapantay-pantay na kasama dito.
2) Ang hanay ng mga solusyon sa hindi pagkakapantay-pantay na f (x; y)> 0 ay maaaring graphical na ilarawan sa coordinate plane. Karaniwan, ang linya na ibinigay ng equation f (x; y) \u003d 0 ay naghahati sa eroplano sa 2 bahagi, ang isa ay ang solusyon sa hindi pagkakapantay-pantay. Upang matukoy kung alin sa mga bahagi, kinakailangan upang palitan ang mga coordinate ng isang di-makatwirang punto M (x0; y0) na hindi namamalagi sa linya f (x; y) \u003d 0 sa hindi pagkakapantay-pantay. Kung f(x0;y0) > 0, kung gayon ang solusyon sa hindi pagkakapantay-pantay ay ang bahagi ng eroplanong naglalaman ng puntong М0. kung f(x0; y0)<0, то другая часть плоскости.
3) Ang hanay ng mga solusyon sa isang sistema ng hindi pagkakapantay-pantay ay ang intersection ng mga hanay ng mga solusyon ng mga hindi pagkakapantay-pantay na kasama dito. Hayaan, halimbawa, ang isang sistema ng hindi pagkakapantay-pantay ay ibigay:
.
Para sa unang hindi pagkakapantay-pantay, ang hanay ng mga solusyon ay isang bilog na may radius na 2 at nakasentro sa pinanggalingan, at para sa pangalawa, isang kalahating eroplano na matatagpuan sa itaas ng linyang 2x+3y=0. Ang hanay ng mga solusyon ng sistemang ito ay ang intersection ng mga set na ito, i.e. kalahating bilog.
4) Halimbawa. Lutasin ang sistema ng hindi pagkakapantay-pantay:
Ang solusyon ng 1st inequality ay ang set , ang 2nd set (2;7) at ang pangatlo - ang set .
Ang intersection ng mga set na ito ay ang interval (2;3], na siyang hanay ng mga solusyon sa sistema ng hindi pagkakapantay-pantay.
5. Solusyon ng mga rational inequalities sa pamamagitan ng interval method
Ang paraan ng agwat ay batay sa sumusunod na katangian ng binomial (x-a): hinahati ng puntong x=α ang totoong axis sa dalawang bahagi - sa kanan ng puntong α, ang binomial (x‑α)>0, at sa kaliwa ng puntong α (x-α)<0.
Hayaang kailanganin na lutasin ang hindi pagkakapantay-pantay (x-α 1)(x-α 2)...(x-α n)>0, kung saan ang α 1 , α 2 ...α n-1 , α n ay naayos mga numero, kung saan walang mga katumbas, at tulad ng α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 sa pamamagitan ng paraan ng mga agwat ay nagpapatuloy tulad ng sumusunod: mga numero α 1 , α 2 ... α n-1 , α n ay inilalapat sa numerical axis; sa puwang sa kanan ng pinakamalaki sa kanila, i.e. mga numero α n , maglagay ng plus sign, sa pagitan na kasunod nito mula kanan papuntang kaliwa ay maglagay ng minus sign, pagkatapos ay plus sign, pagkatapos ay minus sign, atbp. Pagkatapos ang hanay ng lahat ng mga solusyon sa hindi pagkakapantay-pantay (x-α 1)(x-α 2)...(x-α n)>0 ay magiging unyon ng lahat ng mga pagitan kung saan inilalagay ang plus sign, at ang set ng mga solusyon sa hindi pagkakapantay-pantay (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) Solusyon ng mga makatwirang hindi pagkakapantay-pantay (i.e. hindi pagkakapantay-pantay ng anyo 
Ang P(x) Q(x) kung saan ang mga polynomial) ay batay sa sumusunod na katangian ng isang tuluy-tuloy na pag-andar: kung ang isang tuluy-tuloy na pag-andar ay naglaho sa mga puntong x1 at x2 (x1; x2) at wala nang iba pang mga ugat sa pagitan ng mga puntong ito, kung gayon sa ang mga pagitan (x1; x2) ang function ay nagpapanatili ng sign nito.
Samakatuwid, upang mahanap ang mga pagitan ng constancy ng function na y=f(x) sa linya ng numero, markahan ang lahat ng mga punto kung saan ang function na f(x) ay naglalaho o nasira. Hinahati ng mga puntong ito ang totoong linya sa ilang mga pagitan, sa loob ng bawat isa kung saan ang function na f(x) ay tuloy-tuloy at hindi naglalaho, i.e. nagse-save ng sign. Upang matukoy ang sign na ito, sapat na upang mahanap ang sign ng function sa anumang punto ng itinuturing na pagitan ng totoong linya.
2) Upang matukoy ang mga pagitan ng pare-parehong pag-sign ng isang rational function, i.e. Upang malutas ang isang makatwirang hindi pagkakapantay-pantay, minarkahan namin sa linya ng numero ang mga ugat ng numerator at ang mga ugat ng denominator, na, pati na rin ang mga ugat at punto ng discontinuity ng rational function.
Paglutas ng mga hindi pagkakapantay-pantay sa pamamagitan ng paraan ng pagitan
3. 
< 20.
Solusyon. Ang hanay ng mga katanggap-tanggap na halaga ay tinutukoy ng sistema ng hindi pagkakapantay-pantay:
Para sa function na f(x) = – 20. Hanapin ang f(x):
kung saan ang x = 29 at x = 13.
f(30) = – 20 = 0.3 > 0,
f(5) = – 1 – 20 = – 10< 0.
Sagot: . Mga pangunahing pamamaraan para sa paglutas ng mga rational equation. 1) Ang pinakasimpleng: nalutas sa pamamagitan ng karaniwang mga pagpapasimple - pagbawas sa isang karaniwang denominator, pagbabawas ng mga katulad na miyembro, at iba pa. Ang mga parisukat na equation na ax2 + bx + c = 0 ay nalulutas ng...
Ang X ay nagbabago sa pagitan (0,1], at bumababa sa pagitan .
Nakikita natin ang pagdaragdag n sa argumento x, hindi nagbabago
halaga ng function. Pinakamaliit na hindi-zero na numero
mula sa n ay , kaya ito ang period sin 2 x .
Function nulls. Ang halaga ng argumento kung saan ang function ay katumbas ng 0 ay tinatawag zero ( ugat) function. Ang isang function ay maaaring magkaroon ng maramihang mga zero. Halimbawa, ang function y = x (x + 1) (x- 3) ay may tatlong mga zero: x = 0, x = — 1, x= 3. Geometrically function null – ay ang abscissa ng punto ng intersection ng graph ng function na may axis X .
Ipinapakita ng Figure 7 ang graph ng function na may mga zero: x = a , x = b At x = c .
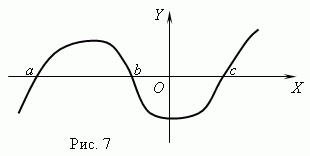
Asymptote. Kung ang graph ng isang function ay lumalapit sa isang tiyak na tuwid na linya nang walang katiyakan habang ito ay lumalayo sa pinanggalingan, ang tuwid na linyang ito ay tinatawag na asymptote.
Paksa 6. "Paraan ng mga pagitan".
Kung f (x) f (x 0) para sa x x 0, kung gayon ang function na f (x) ay tinatawag tuloy-tuloy sa x 0.
Kung ang isang function ay tuloy-tuloy sa bawat punto ng ilang interval I, kung gayon ito ay tinatawag tuloy-tuloy sa pagitan Ako (ang pagitan na tinatawag na ako agwat ng pagpapatuloy ng function). Ang graph ng function sa interval na ito ay isang tuluy-tuloy na linya, na sinasabing "iginuhit nang hindi inaangat ang lapis mula sa papel."
Pag-aari ng tuluy-tuloy na pag-andar.
Kung sa pagitan (a ; b) ang function na f ay tuloy-tuloy at hindi naglalaho, kung gayon nananatili itong isang pare-parehong tanda sa pagitan na ito.
Ang paraan ng paglutas ng mga hindi pagkakapantay-pantay sa isang variable ay batay sa ari-arian na ito - ang paraan ng mga agwat. Hayaang maging tuluy-tuloy ang function na f(x) sa interval I at maglaho sa isang may hangganang bilang ng mga puntos sa interval na ito. Sa pamamagitan ng pag-aari ng tuluy-tuloy na pag-andar, ang mga puntong ito ay naghahati sa I sa mga pagitan, sa bawat isa kung saan ang tuluy-tuloy na pag-andar f(x) c ay nagbabantay ng isang palaging tanda. Upang matukoy ang sign na ito, sapat na upang kalkulahin ang halaga ng function na f(x) sa anumang isang punto mula sa bawat ganoong pagitan. Batay dito, nakuha namin ang sumusunod na algorithm para sa paglutas ng mga hindi pagkakapantay-pantay sa pamamagitan ng paraan ng agwat.
Ang paraan ng pagitan para sa mga hindi pagkakapantay-pantay ng anyo
paraan ng pagitan. Average na antas.
Gusto mo bang subukan ang iyong lakas at malaman ang resulta kung gaano ka kahanda para sa Unified State Examination o sa OGE?
Linear function
Ang isang function ng form ay tinatawag na linear. Kunin natin ang isang function bilang isang halimbawa. Ito ay positibo sa 3″> at negatibo sa. Ang punto ay ang zero ng function (). Ipakita natin ang mga palatandaan ng pagpapaandar na ito sa totoong axis:
Sinasabi namin na "nagbabago ang function ng sign kapag dumadaan sa isang punto".
Makikita na ang mga palatandaan ng function ay tumutugma sa posisyon ng graph ng function: kung ang graph ay nasa itaas ng axis, ang sign ay " ", kung ito ay nasa ibaba nito, " ".
Kung i-generalize natin ang resultang panuntunan sa isang arbitrary linear function, makukuha natin ang sumusunod na algorithm:
quadratic function
Sana naaalala mo kung paano nalulutas ang mga quadratic inequalities? Kung hindi, basahin ang paksang "Square inequalities". Hayaan akong ipaalala sa iyo ang pangkalahatang anyo ng isang quadratic function: .
Ngayon, tandaan natin kung anong mga palatandaan ang kinukuha ng quadratic function. Ang graph nito ay isang parabola, at ang function ay tumatagal ng sign na “ ” para sa mga kung saan ang parabola ay nasa itaas ng axis, at “ ” - kung ang parabola ay nasa ibaba ng axis:
Kung ang function ay may mga zero (mga halaga kung saan), ang parabola ay nag-intersect sa axis sa dalawang punto - ang mga ugat ng kaukulang quadratic equation. Kaya, ang axis ay nahahati sa tatlong agwat, at ang mga palatandaan ng pag-andar ay nagbabago nang halili kapag dumadaan sa bawat ugat.
Posible bang matukoy ang mga palatandaan nang walang pagguhit ng parabola sa bawat oras?
Alalahanin na ang square trinomial ay maaaring i-factorize:
Tandaan ang mga ugat sa axis:
Naaalala namin na ang tanda ng isang function ay maaari lamang magbago kapag dumadaan sa ugat. Ginagamit namin ang katotohanang ito: para sa bawat isa sa tatlong mga agwat kung saan ang axis ay nahahati sa mga ugat, sapat na upang matukoy ang tanda ng pag-andar lamang sa isang arbitraryong napiling punto: sa iba pang mga punto ng agwat, ang palatandaan ay ang pareho.
Sa aming halimbawa: para sa 3″> parehong mga expression sa mga bracket ay positibo (pinapalitan namin, halimbawa: 0″>). Inilalagay namin ang sign na "" sa axis:
Well, kung (kapalit, halimbawa) ang parehong mga bracket ay negatibo, kung gayon ang produkto ay positibo:
Iyon na iyon paraan ng pagitan: alam ang mga palatandaan ng mga kadahilanan sa bawat pagitan, tinutukoy namin ang tanda ng buong produkto.
Isaalang-alang din natin ang mga kaso kapag ang function ay walang mga zero, o ito ay isa lamang.
Kung wala, kung gayon walang mga ugat. Nangangahulugan ito na walang "daanan sa ugat". Nangangahulugan ito na ang function sa buong axis ng numero ay tumatagal lamang ng isang senyas. Madaling matukoy sa pamamagitan ng pagpapalit nito sa isang function.
Kung mayroon lamang isang ugat, ang parabola ay humipo sa axis, kaya ang tanda ng pag-andar ay hindi nagbabago kapag dumadaan sa ugat. Ano ang panuntunan para sa mga ganitong sitwasyon?
Kung isasaalang-alang natin ang gayong pag-andar, makakakuha tayo ng dalawang magkaparehong salik:
At ang anumang parisukat na expression ay hindi negatibo! Samakatuwid, ang tanda ng pag-andar ay hindi nagbabago. Sa ganitong mga kaso, pipiliin namin ang ugat, kapag dumadaan kung saan ang tanda ay hindi nagbabago, pinaikot ito ng isang parisukat:
Ang gayong ugat ay tatawagin maramihan.
Ang paraan ng mga agwat sa hindi pagkakapantay-pantay
Ngayon ang anumang quadratic inequality ay malulutas nang hindi gumuhit ng parabola. Ito ay sapat lamang upang ilagay ang mga palatandaan ng quadratic function sa axis, at piliin ang mga agwat depende sa hindi pagkakapantay-pantay na palatandaan. Halimbawa:
Sinusukat namin ang mga ugat sa axis at ayusin ang mga palatandaan:
Kailangan namin ang bahagi ng axis na may sign na ""; dahil ang hindi pagkakapantay-pantay ay hindi mahigpit, ang mga ugat mismo ay kasama rin sa solusyon:
Ngayon isaalang-alang ang isang makatwirang hindi pagkakapantay-pantay - isang hindi pagkakapantay-pantay, ang parehong bahagi nito ay mga makatwirang expression (tingnan ang "Rational Equation").
Halimbawa:
Ang lahat ng mga kadahilanan maliban sa isa - - narito ang "linear", iyon ay, naglalaman ang mga ito ng variable lamang sa unang antas. Kailangan namin ang mga linear na kadahilanan upang mailapat ang paraan ng agwat - nagbabago ang tanda kapag dumadaan sa kanilang mga ugat. Ngunit ang multiplier ay walang mga ugat sa lahat. Nangangahulugan ito na ito ay palaging positibo (suriin ito sa iyong sarili), at samakatuwid ay hindi nakakaapekto sa tanda ng buong hindi pagkakapantay-pantay. Nangangahulugan ito na maaari mong hatiin ang kaliwa at kanang bahagi ng hindi pagkakapantay-pantay dito, at sa gayon ay mapupuksa ito:
Ngayon ang lahat ay pareho sa mga quadratic na hindi pagkakapantay-pantay: tinutukoy namin kung anong mga punto ang bawat isa sa mga kadahilanan ay naglalaho, markahan ang mga puntong ito sa axis at ayusin ang mga palatandaan. Iginuhit ko ang iyong pansin sa isang napakahalagang katotohanan:
Sa kaso ng isang kahit na numero, nagpapatuloy kami sa parehong paraan tulad ng dati: bilugan namin ang punto na may isang parisukat at hindi binabago ang tanda kapag dumadaan sa ugat. Ngunit sa kaso ng isang kakaibang numero, ang panuntunang ito ay hindi natutupad: ang tanda ay magbabago pa rin kapag dumaan sa ugat. Samakatuwid, wala kaming ginagawang karagdagan sa gayong ugat, na parang hindi ito maramihan sa amin. Ang mga tuntunin sa itaas ay nalalapat sa lahat ng pantay at kakaibang kapangyarihan.
Ano ang isusulat natin sa sagot?
Kung ang paghahalili ng mga palatandaan ay nilabag, kailangan mong maging maingat, dahil sa hindi mahigpit na hindi pagkakapantay-pantay, ang sagot ay dapat isama lahat ng punong puntos. Ngunit ang ilan sa kanila ay madalas na nag-iisa, iyon ay, hindi sila pumapasok sa lilim na lugar. Sa kasong ito, idinaragdag namin sila sa tugon bilang mga hiwalay na tuldok (sa mga kulot na brace):
Mga halimbawa (magpasya para sa iyong sarili):
Mga sagot:
- Kung kabilang sa mga kadahilanan ito ay simple - ito ang ugat, dahil maaari itong ilarawan bilang.
.
Ano ang mga function zero? Ang sagot ay medyo simple - ito ay isang mathematical term, na nangangahulugang ang domain ng isang naibigay na function, kung saan ang halaga nito ay zero. Ang mga function na zero ay tinatawag ding Function zeros Ang pinakamadaling paraan upang ipaliwanag kung ano ang mga function na zero ay sa pamamagitan ng ilang simpleng halimbawa.
Mga halimbawa
Isaalang-alang ang isang simpleng equation na y=x+3. Dahil ang zero ng function ay ang halaga ng argument kung saan naging zero ang y, pinapalitan namin ang 0 sa kaliwang bahagi ng equation:
Sa kasong ito, -3 ang nais na zero. Para sa isang ibinigay na function, mayroon lamang isang ugat ng equation, ngunit hindi ito palaging ang kaso.
Isaalang-alang ang isa pang halimbawa:
Palitan ang 0 sa kaliwang bahagi ng equation, tulad ng sa nakaraang halimbawa:
Malinaw, sa kasong ito, magkakaroon ng dalawang zero ng function: x=3 at x=-3. Kung ang equation ay may argumento ng ikatlong antas, magkakaroon ng tatlong zero. Maaari tayong gumawa ng isang simpleng konklusyon na ang bilang ng mga ugat ng polynomial ay tumutugma sa pinakamataas na antas ng argumento sa equation. Gayunpaman, maraming mga function, halimbawa y=x 3 , sa unang tingin ay sumasalungat sa pahayag na ito. Iminumungkahi ng lohika at sentido komun na ang function na ito ay may isang zero lamang - sa puntong x=0. Ngunit sa katunayan mayroong tatlong ugat, lahat sila ay nagtutugma. Kung malulutas mo ang equation sa kumplikadong anyo, ito ay nagiging halata. x=0 sa kasong ito, ang ugat, ang multiplicity ng kung saan ay 3. Sa nakaraang halimbawa, ang mga zero ay hindi tumugma, samakatuwid mayroon silang multiplicity ng 1.
Definition algorithm
Mula sa ipinakita na mga halimbawa ay malinaw kung paano matukoy ang mga zero ng function. Ang algorithm ay palaging pareho:
- Sumulat ng isang function.
- Palitan ang y o f(x)=0.
- Lutasin ang resultang equation.
Ang pagiging kumplikado ng huling item ay nakasalalay sa antas ng argumento ng equation. Kapag nilulutas ang mga equation na may mataas na degree, lalong mahalaga na tandaan na ang bilang ng mga ugat ng equation ay katumbas ng pinakamataas na kapangyarihan ng argumento. Ito ay totoo lalo na para sa trigonometric equation, kung saan ang paghahati ng parehong bahagi sa pamamagitan ng sine o cosine ay humahantong sa pagkawala ng mga ugat.
Ang mga arbitrary degree equation ay pinakamadaling malutas sa pamamagitan ng pamamaraan ni Horner, na partikular na binuo para sa paghahanap ng mga zero ng isang arbitraryong polynomial.
Ang halaga ng mga zero ng mga function ay maaaring parehong negatibo at positibo, totoo o nakahiga sa kumplikadong eroplano, iisa o maramihan. O maaaring walang mga ugat ng equation. Halimbawa, ang function na y=8 ay hindi magiging zero para sa anumang x, dahil hindi ito nakadepende sa variable na ito.
Ang equation na y=x 2 -16 ay may dalawang ugat, at parehong nasa kumplikadong eroplano: x 1 =4i, x 2 =-4i.
Mga karaniwang pagkakamali
Ang isang karaniwang pagkakamali na ginawa ng mga mag-aaral na hindi pa talaga nakakaalam kung ano ang mga zero ng isang function ay ang pagpapalit ng argumento (x) ng zero, at hindi ang halaga (y) ng function. Kumpiyansa nilang pinapalitan ang x = 0 sa equation at, batay dito, hanapin ang y. Ngunit ito ay maling diskarte.
Ang isa pang pagkakamali, tulad ng nabanggit na, ay ang pagbabawas ng sine o cosine sa trigonometric equation, kaya naman nawala ang isa o higit pang mga zero ng function. Hindi ito nangangahulugan na walang maaaring bawasan sa mga naturang equation, ngunit ang mga "nawawalang" salik na ito ay dapat isaalang-alang sa karagdagang mga kalkulasyon.
Grapikal na presentasyon
Maiintindihan mo kung ano ang mga zero ng isang function sa tulong ng mga mathematical program tulad ng Maple. Sa loob nito, maaari kang bumuo ng isang graph sa pamamagitan ng pagtukoy ng nais na bilang ng mga puntos at ang nais na sukat. Ang mga puntong iyon kung saan tumatawid ang graph sa axis ng OX ay ang mga gustong zero. Ito ay isa sa pinakamabilis na paraan upang mahanap ang mga ugat ng isang polynomial, lalo na kung ang pagkakasunud-sunod nito ay mas mataas kaysa sa ikatlo. Kaya't kung may pangangailangan na regular na magsagawa ng mga kalkulasyon sa matematika, hanapin ang mga ugat ng polynomial ng mga di-makatwirang degree, bumuo ng mga graph, Maple o isang katulad na programa ay kailangang-kailangan para sa pagsasagawa at pag-verify ng mga kalkulasyon.
Algorithm paraan ng pagitan simple at hindi sopistikado:
1) Hanapin saklaw ng function.
2) Hanapin function na mga zero(mga punto ng intersection ng graph sa x-axis).
3) Karamihan sa mga trabaho ay mangangailangan ng blueprint. Gumuhit kami ng isang axis at mag-plot ng mga break point dito (kung mayroon man), pati na rin ang mga zero ng function (kung mayroon man). Tinutukoy namin ang mga palatandaan ng pag-andar sa mga pagitan na kasama sa domain ng kahulugan.
Maaari mong balangkasin ang mga punto, gayunpaman, maaalala ng algorithm ang kahit isang buong takure nang napakabilis. Ang lahat ay transparent at lohikal dito.
Magsimula tayo sa isang karaniwang quadratic function:
Halimbawa 1
Maghanap ng mga pagitan ng constancy ng function. 
Solusyon:
1) Ang function ay tinukoy at tuloy-tuloy sa buong tunay na linya. kaya, break points at walang "masamang" gaps.
2) Hanapin ang mga zero ng function. Upang gawin ito, kailangan mong lutasin ang equation. Sa kasong ito: 
Ang discriminant ay positibo, kaya ang equation ay may dalawang tunay na ugat: 
3) Itabi ang lahat ng nahanap na punto sa numerical axis:
Sa artikulo Saklaw ng pag-andar Gumawa ako ng gayong mga guhit sa eskematiko, ngunit ngayon para sa higit na kalinawan ng pagtatanghal ay susukatin ko ang mga ito (maliban sa mga klinikal na kaso). Sa parehong aralin, natutunan namin kung paano malaman ang mga palatandaan ng isang function sa mga pagitan - maaari mong pag-aralan ang lokasyon ng parabola. Sa kasong ito, ang mga sanga ng parabola ay nakadirekta paitaas, samakatuwid, sa mga pagitan 
magiging positibo ang function: . Ang ilalim ng parabola ay nakaupo sa pagitan sa ibaba ng x-axis, at ang function dito ay negatibo: .
Well, maraming mga mambabasa ang nag-iisip ng isang parabola. Ngunit paano kung ang pag-andar ay mas kumplikado? Halimbawa, . Ang isang kapansin-pansing bahagi ng madla ay mahihirapang sabihin kung ano ang hitsura ng graph ng function na ito sa panimula. At ito, kumbaga, ay kaunting komplikasyon lamang.
Gayunpaman, sa parehong simple at kumplikadong mga kaso, gumagana ang unibersal na pamamaraan:
Isaalang-alang ang isang tuluy-tuloy na function sa ilang interval , na ang graph ay hindi nagsalubong sa axis sa interval na ito. Pagkatapos:
Kung ang function positibo sa ilang punto ng pagitan , pagkatapos ito ay positibo at SA LAHAT mga punto ng agwat na ito;
Kung ang function negatibo sa anumang punto ng pagitan , pagkatapos ito ay negatibo at SA LAHAT mga punto ng agwat na ito.
I-on ang isang maliit na imahinasyon: kung walang mga breakpoint sa pagitan, at ang graph ay hindi tumatawid sa x-axis, hindi ito maaaring magically tumalon mula sa lower half-plane patungo sa upper half-plane (o vice versa). Samakatuwid, ang tanda ng pag-andar sa naturang pagitan ay madaling matukoy mula sa isang punto.
Gumawa tayo ng isang maliit na eksperimento. Isipin na hindi mo alam kung ano ang hitsura ng graph ng isang function. at kailangan mong hanapin ang mga agwat ng katatagan nito (nga pala, kung talagang hindi mo alam, gumuhit ng mahabang pagtitiis na prima donna =)).
1) Kumuha kami ng di-makatwirang punto ng pagitan . Mula sa isang computational point of view, ito ay pinakamadaling kunin . Isaksak natin ito sa ating function:
Samakatuwid, ang pag-andar ay positibo at sa bawat punto ng pagitan.
2) Kumuha kami ng di-makatwirang punto ng pagitan , dito, para sa kaginhawahan, wala sa kompetisyon ang zero.
Ginagawa namin muli ang pagpapalit:
Kaya ang function ay negatibo at sa bawat punto ng pagitan.
3) At sa wakas, pinoproseso namin ang pinakasimpleng punto ng agwat:
Kaya ang pag-andar ay positibo. sa bawat punto ng pagitan.
Ang mga isinagawang pagpapalit, ang mga kalkulasyon ay halos palaging madaling gawin sa salita, ngunit sa matinding mga kaso mayroon ding draft.
Inaayos namin ang mga resulta sa numerical axis:
Oo, wala kang ideya tungkol sa parabola, ngunit tiyak na masasabi mo iyon sa mga pagitan 
function graph matatagpuan sa ITAAS ng axis, at sa pagitan - SA IBABA ng axis na ito.
Sagot:
Kung ;
, Kung .
Sa parehong paraan, ang isang buong hanay ng mga "satellite" na gawain ay nalutas, narito ang ilan sa mga ito:
.
Nagsasagawa kami ng mga katulad na aksyon at nagbibigay ng sagot 
.
Lutasin ang quadratic inequality .
Nagsasagawa kami ng mga katulad na aksyon at nagbibigay ng sagot.
Hanapindomain
mga function 
.
Nagsasagawa kami ng mga katulad na aksyon, nagbibigay kami ng sagot.
Gumagana ang paraan ng agwat sa pinaka primitive na mga kaso, halimbawa, para sa . Dito, ang tuwid na linya ay nag-intersect sa abscissa axis sa punto , habang sa kaliwa ng puntong ito (ang graph ay nasa ibaba ng axis), at sa kanan (ang graph ay nasa itaas ng axis). Gayunpaman, para sa mga nasa tangke, ang problema ay malulutas din sa pamamagitan ng paraan ng agwat.
Maaari bang maging positibo o negatibo ang isang function sa buong linya ng numero? Siyempre, sa artikulo Saklaw ng pag-andar tumingin kami sa mga karaniwang halimbawa. Sa partikular, ito ay natagpuan na 
(isang parabola na ganap na nakahiga sa itaas na kalahating eroplano). Ang paraan ng mga pagitan ay pumasa at dito! Isinasaalang-alang namin ang tanging agwat , kunin ang pinaka-maginhawang punto mula dito at gawin ang pagpapalit: 
. Nangangahulugan ito na ang function ay positibo sa bawat punto ng pagitan.